Heskestad módszere alkalmas nyílt téri tűz vizsgálatára is, ebben a gyakorlati esetben a H-érték jelentőségét veszti, mivel nincs felső födém az alkalmazott modellben.
A gyakorlati számítás első lépéseként a láng hosszát kell meghatározni, amely a 28. képlet segítségével lehetséges.

ahol:
Lf: a lokális tűz lángjának hossza [m],
D: a tűz átmérője [m],
Q: a tűz hőkibocsátása [W].
A tűz hőkibocsátásának meghatározását fentebb tárgyaltuk részletesen.
A tűz hőkibocsátásának ismeretében meghatározható annak konvekciós része, amelyet a szabvány alapján a tűz hőkibocsátásának 80%-ával lehet közelíteni a 29. képlet alapján. Valamint számítható a 30. képlet szerint a láng tengelyének z0 kiindulópontja is.

ahol:
Qc: a tűz hőkibocsátásának konvekciós része [W],
Q: a tűz hőkibocsátása [W].

ahol:
z0: a láng tengelyének z0 kiindulópontja [m],
D: a tűz átmérője [m],
Q: a tűz hőkibocsátása [W].
Meghatározva a 29. és 30. képletek szerinti segédmennyiségeket, számíthatóvá válik a 31. képlet szerint a láng függőleges tengelye mentén az izzó gáz hőmérséklete. A képlet abban az esetben igaz, ha a láng nem éri el a födémet vagy nyílt téri tűz vizsgálatára van szükség.

ahol:
Θ(z): a láng tengelye mentén izzó gáz hőmérséklete a vizsgált z magasságban [m],
Qc: a tűz hőkibocsátásának konvekciós része [W],
z: a láng tengelye mentén mért z magasság a vizsgált pontban [m],
z0: a láng tengelyének z0 kiindulópontja [m].
Mivel cikkünkben a födémekre alkalmazzuk a lokális tűzhatást, így a 31. képlet a z=H helyettesítés révén a 32. képletre módosul.

ahol:
Θ(H): az izzó gáz hőmérséklete a födém alsó síkján [m],
H: a tűz forrása és a födém alsó síkja közötti távolság [m].
Amikor a láng eléri a felső födémet, abban az esetben Hasemi módszerét kell alkalmazni. A modellhez tartozó geometriai paramétereket a 4. ábra szemlélteti. Ebben az esetben az y paraméter függvényében a födém egységnyi felületére átadódó hőáramot [W/m2] a 33. képlet alapján lehet figyelembe venni.

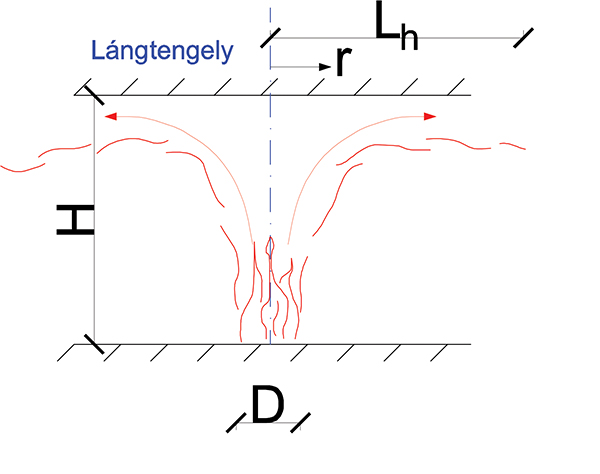
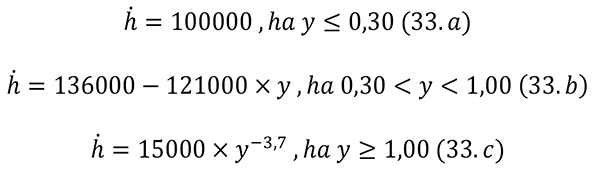
A 4. ábra jelölései a következők:
H: a tűz forrása és a födém alsó síkja közötti távolság [m],
Lh: a lokális tűz lángjának vízszintes hossza [m],
r: a láng tengelyétől a mennyezet azon pontjáig mért vízszintes távolság, ahol a hőáram számítása történik [m],
D: a tűz átmérője [m].
Az y paraméter a 34. képlet segítségével határozható meg.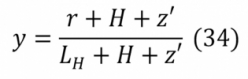

ahol:
H: a tűz forrása és a födém alsó síkja közötti távolság [m],
Lh: a lokális tűz lángjának vízszintes hossza [m],
r: a láng tengelyétől a mennyezet azon pontjáig mért vízszintes távolság, ahol a hőáram számítása történik [m],
z’: a virtuális hőforráshoz képest mért helykoordináta [m].